Stats for a full-frame 35mm camera, taken from lens manufacturers' spec sheets.
- 50mm = 46 degrees
- 70mm = 34 degrees
- 135mm = 18 degrees
- 200mm = 12 degrees
Now, those are presumably across a circular diameter (ie. the diagonal of a frame).
For a 3m wide backdrop, your hypotenuse in 3:2 aspect ratio is sqrt(13), or 3.6m.
Now use some trig to convert those angles into 3.6m.
Working in landscape orientation
For a 50mm lens
- theta = 23 degrees
- Opposite = 180cm
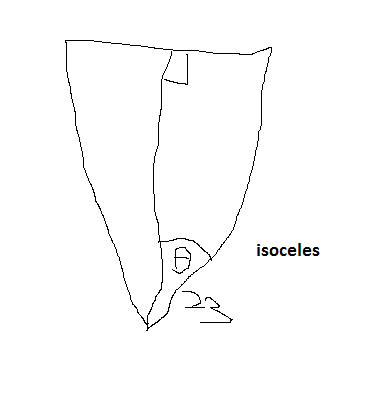
tan(23 degrees) = 180 / working distance 0.42 = 180 / working distance 1/0.42 = working distance / 180 180/0.42 = working distance working distance = 428cm?
4.3 metres
My mathematical gut feeling says this is wrong... but it seems about right when I hold the 50mm up to my eye.
70mm lens
theta = 17 degrees
working distance = 180 / tan(17)
= 180 / 0.306
= 588cm5.9 metres
135mm lens
theta = 9 degrees
working distance = 180 / tan(9)
= 180 / 0.158
= 1136cm11.3 metres
200mm lens
theta = 6 degrees
working distance = 180 / tan(6)
= 180 / 0.105
= 1712cm17.1 metres