Stats for a full-frame 35mm camera, taken from lens manufacturers' spec sheets.
- 50mm = 46 degrees
- 70mm = 34 degrees
- 85mm = 28 degrees
- 135mm = 18 degrees
- 200mm = 12 degrees
Now, those are presumably across a circular diameter (ie. the diagonal of a frame).
Contents
Working in landscape orientation
For a 3m wide backdrop, your hypotenuse in 3:2 aspect ratio is sqrt(13), or 3.6m.
Now use some trig to convert those angles into 3.6m.
Cheating: divide your focal length (mm) by 11.76 to get the distance in metres
For a 50mm lens
- theta = 23 degrees
- Opposite = 180cm
tan(23 degrees) = 180 / working distance 0.42 = 180 / working distance 1/0.42 = working distance / 180 180/0.42 = working distance working distance = 428cm?
4.3 metres
My mathematical gut feeling says this is wrong... but it seems about right when I hold the 50mm up to my eye.
70mm lens
theta = 17 degrees
working distance = 180 / tan(17)
= 180 / 0.306
= 588cm5.9 metres
85mm lens
Working distance = 180 / 0.249 = 7.23 metres
135mm lens
theta = 9 degrees
working distance = 180 / tan(9)
= 180 / 0.158
= 1136cm11.3 metres
200mm lens
theta = 6 degrees
working distance = 180 / tan(6)
= 180 / 0.105
= 1712cm17.1 metres
Working in portrait orientation
For a 3m wide backdrop, your hypotenuse in 2:3 aspect ratio is sqrt(29.25), or 5.4m.
Now use some trig to convert those angles into 5.4m.
Cheating: divide your focal length (mm) by 7.87 to get the distance in metres
For a 50mm lens
theta = 23 degrees
working distance = 270 / tan(23)
= 270 / 0.424
= 636cm6.3 metres
70mm lens
theta = 17 degrees
working distance = 270 / tan(17)
= 270 / 0.306
= 883cm8.8 metres
85mm lens
Working distance = 270 / 0.249 = 10.8 metres
135mm lens
theta = 9 degrees
working distance = 270 / tan(9)
= 270 / 0.158
= 1704cm17 metres
200mm lens
theta = 6 degrees
working distance = 270 / tan(6)
= 270 / 0.105
= 2568cm25.6 metres
Portrait mode with 2m fixed height subject
- 2m high
- 1.33m wide
2.4m diagonal
- 1.2m for right-angle triangle (120cm)
Cheating: divide your focal length (mm) by 17.71 to get the distance in metres
50mm lens
- theta = 23 degrees
- working distance = 120 / tan(23)
2.82 metres
70mm lens
Working distance = 120 / 0.306 = 3.92 metres
85mm lens
Working distance = 120 / 0.249 = 4.82 metres
135mm lens
Working distance = 120 / 0.158 = 7.59 metres
200mm lens
Working distance = 120 / 0.105 = 11.4 metres
In a table
|
3m landscape max. |
2m portrait max. |
2m fixed-height subject |
50mm |
4.3 |
6.3 |
2.8 |
70mm |
5.9 |
8.8 |
3.9 |
85mm |
7.2 |
10.8 |
4.8 |
135mm |
11.3 |
17.0 |
7.6 |
200mm |
17.1 |
25.6 |
11.4 |
Diagrams
Working room for subject
Assuming a 2m high subject, and a 3m x 3m backdrop, we have a certain amount of room to play with.
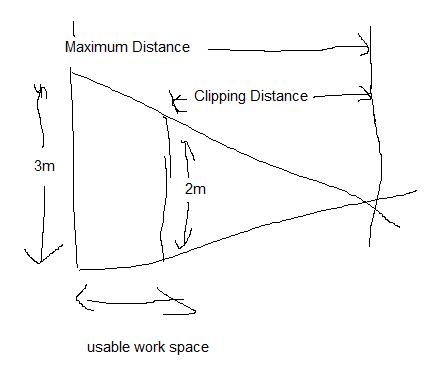
Using the figures from the table, and assuming portrait mode:
- Photographer can move back as far away as the second column ("2m portrait max.")
- Subject must be further from photographer than the distance in the third column (aka. "clipping distance")
- Subject could be right up against the backdrop, in theory
$col3 - $col2 = playspace
|
2m portrait max. |
Clipping distance |
Playspace in metres |
50mm |
6.3 |
2.8 |
3.5 |
70mm |
8.8 |
3.9 |
4.9 |
85mm |
10.8 |
4.8 |
6.0 |
135mm |
17.0 |
7.6 |
9.4 |
200mm |
25.6 |
11.4 |
14.2 |