|
Size: 702
Comment: 50mm working
|
Size: 2741
Comment: added fixed-height subject
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 8: | Line 8: |
| Now, those are presumably across a circular diameter (ie. the diagonal of a frame). | |
| Line 9: | Line 10: |
| Now, those are presumably across a circular diameter (ie. the diagonal of a frame). | <<TableOfContents>> = Working in landscape orientation = |
| Line 16: | Line 21: |
| = Working = For a 50mm lens: |
== For a 50mm lens == |
| Line 21: | Line 24: |
{{attachment:50mm_triangle.png}} |
|
| Line 34: | Line 39: |
| I don't think this is correct... | '''4.3 metres''' My mathematical gut feeling says this is wrong... but it seems about right when I hold the 50mm up to my eye. == 70mm lens == {{{ theta = 17 degrees working distance = 180 / tan(17) = 180 / 0.306 = 588cm }}} '''5.9 metres''' == 135mm lens == {{{ theta = 9 degrees working distance = 180 / tan(9) = 180 / 0.158 = 1136cm }}} '''11.3 metres''' == 200mm lens == {{{ theta = 6 degrees working distance = 180 / tan(6) = 180 / 0.105 = 1712cm }}} '''17.1 metres''' = Working in portrait orientation = For a 3m wide backdrop, your hypotenuse in 2:3 aspect ratio is sqrt(29.25), or 5.4m. Now use some trig to convert those angles into 5.4m. == For a 50mm lens == {{{ theta = 23 degrees working distance = 270 / tan(23) = 270 / 0.424 = 636cm }}} '''6.3 metres''' == 70mm lens == {{{ theta = 17 degrees working distance = 270 / tan(17) = 270 / 0.306 = 883cm }}} '''8.8 metres''' == 135mm lens == {{{ theta = 9 degrees working distance = 270 / tan(9) = 270 / 0.158 = 1704cm }}} '''17 metres''' == 200mm lens == {{{ theta = 6 degrees working distance = 270 / tan(6) = 270 / 0.105 = 2568cm }}} '''25.6 metres''' = Portrait mode with 2m fixed height subject = * 2m high * 1.33m wide * '''2.4m diagonal''' * 1.2m for right-angle triangle (120cm) == 50mm lens == * theta = 23 degrees * working distance = 120 / tan(23) * '''2.82 metres''' == 70mm lens == Working distance = 120 / 0.306 = '''3.92 metres''' == 135mm lens == Working distance = 120 / 0.158 = '''7.59 metres''' == 200mm lens == Working distance = 120 / 0.105 = '''11.4 metres''' |
Stats for a full-frame 35mm camera, taken from lens manufacturers' spec sheets.
- 50mm = 46 degrees
- 70mm = 34 degrees
- 135mm = 18 degrees
- 200mm = 12 degrees
Now, those are presumably across a circular diameter (ie. the diagonal of a frame).
Contents
Working in landscape orientation
For a 3m wide backdrop, your hypotenuse in 3:2 aspect ratio is sqrt(13), or 3.6m.
Now use some trig to convert those angles into 3.6m.
For a 50mm lens
- theta = 23 degrees
- Opposite = 180cm
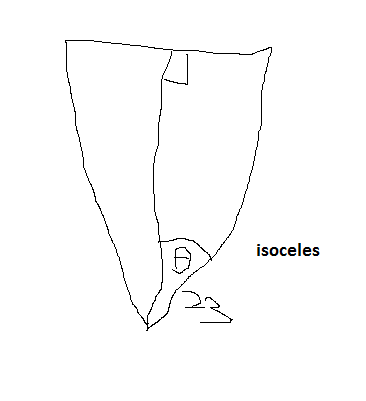
tan(23 degrees) = 180 / working distance 0.42 = 180 / working distance 1/0.42 = working distance / 180 180/0.42 = working distance working distance = 428cm?
4.3 metres
My mathematical gut feeling says this is wrong... but it seems about right when I hold the 50mm up to my eye.
70mm lens
theta = 17 degrees
working distance = 180 / tan(17)
= 180 / 0.306
= 588cm5.9 metres
135mm lens
theta = 9 degrees
working distance = 180 / tan(9)
= 180 / 0.158
= 1136cm11.3 metres
200mm lens
theta = 6 degrees
working distance = 180 / tan(6)
= 180 / 0.105
= 1712cm17.1 metres
Working in portrait orientation
For a 3m wide backdrop, your hypotenuse in 2:3 aspect ratio is sqrt(29.25), or 5.4m.
Now use some trig to convert those angles into 5.4m.
For a 50mm lens
theta = 23 degrees
working distance = 270 / tan(23)
= 270 / 0.424
= 636cm6.3 metres
70mm lens
theta = 17 degrees
working distance = 270 / tan(17)
= 270 / 0.306
= 883cm8.8 metres
135mm lens
theta = 9 degrees
working distance = 270 / tan(9)
= 270 / 0.158
= 1704cm17 metres
200mm lens
theta = 6 degrees
working distance = 270 / tan(6)
= 270 / 0.105
= 2568cm25.6 metres
Portrait mode with 2m fixed height subject
- 2m high
- 1.33m wide
2.4m diagonal
- 1.2m for right-angle triangle (120cm)
50mm lens
- theta = 23 degrees
- working distance = 120 / tan(23)
2.82 metres
70mm lens
Working distance = 120 / 0.306 = 3.92 metres
135mm lens
Working distance = 120 / 0.158 = 7.59 metres
200mm lens
Working distance = 120 / 0.105 = 11.4 metres